Improving Global Optimization in HSVM and SDP Problems
Table of Links
Abstract and 1. Introduction
-
Related Works
-
Convex Relaxation Techniques for Hyperbolic SVMs
3.1 Preliminaries
3.2 Original Formulation of the HSVM
3.3 Semidefinite Formulation
3.4 Moment-Sum-of-Squares Relaxation
-
Experiments
4.1 Synthetic Dataset
4.2 Real Dataset
-
Discussions, Acknowledgements, and References
\
A. Proofs
B. Solution Extraction in Relaxed Formulation
C. On Moment Sum-of-Squares Relaxation Hierarchy
D. Platt Scaling [31]
E. Detailed Experimental Results
F. Robust Hyperbolic Support Vector Machine
3.4 Moment-Sum-of-Squares Relaxation
The SDP relaxation in Equation (8) may not be tight, particularly when the resulting W has a rank much larger than 1. Indeed, we often find W to be full-rank empirically. In such cases, moment-sum-of-squares relaxation may be beneficial. Specifically, it can certifiably find the global optima, provided that the solution exhibits a special structure, known as the flat-extension property [30, 32].
\ 
\ With all these definitions established, we can present the moment-sum-of-squares relaxation [9] to the HSVM problem, outlined in Equation (7), as
\ 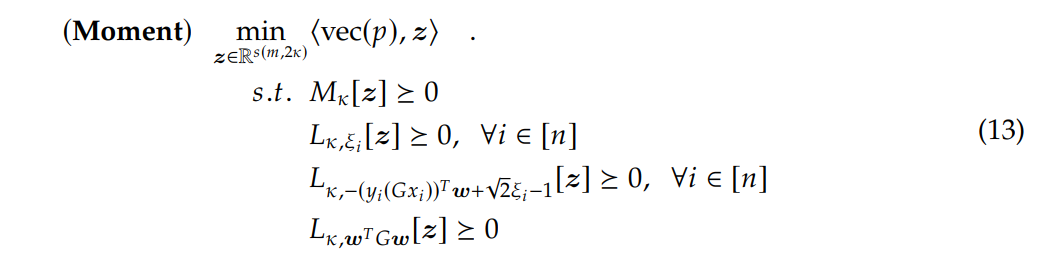
\ Note that 𝑔(q) ⩾ 0, as previously defined, serves as constraints in the original formulation. Additionally, when forming the moment matrix, the degree of generated monomials is 𝑠 = 𝜅 − 1, since all constraints in Equation (7) has maximum degree 1. Consequently, Equation (13) is a convex programming and can be implemented as a standard SDP problem using mainstream solvers. We further emphasize that by progressively increasing the relaxation order 𝜅, we can find increasingly better solutions theoretically, as suggested by Lasserre [33]
\ 
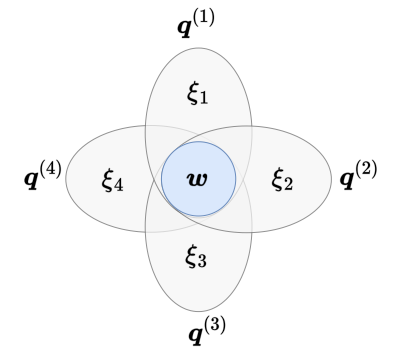
\ where 𝐵 is an index set of the moment matrix to entries generated by w along, ensuring that each moment matrix with overlapping regions share the same values as required. We refer the last constraint as the sparse-binding constraint.
\ Unfortunately, our solution empirically does not satisfy the flat-extension property and we cannot not certify global optimality. Nonetheless, in practice, it achieves significant performance improvements in selected datasets over both projected gradient descent and the SDP-relaxed formulation. Similarly, this formulation does not directly yield decision boundaries and we defer discussions on the extraction methods to Appendix B.2.
\ 
\
:::info Authors:
(1) Sheng Yang, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA (shengyang@g.harvard.edu);
(2) Peihan Liu, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA (peihanliu@fas.harvard.edu);
(3) Cengiz Pehlevan, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA, Center for Brain Science, Harvard University, Cambridge, MA, and Kempner Institute for the Study of Natural and Artificial Intelligence, Harvard University, Cambridge, MA (cpehlevan@seas.harvard.edu).
:::
:::info This paper is available on arxiv under CC by-SA 4.0 Deed (Attribution-Sharealike 4.0 International) license.
:::
\
You May Also Like

Polygon Tops RWA Rankings With $1.1B in Tokenized Assets

The Role of Reference Points in Achieving Equilibrium Efficiency in Fair and Socially Just Economies
![Top Crypto Saving Accounts in Europe 2026 [Regulated and Trusted]](https://images.cryptodaily.co.uk/space/755img.png)
